2 BASIC WAVE MOTION
The sine (or cosine) function defines what is called a regular wave. In order to specify a regular wave we need its amplitude, a, its wavelength, l, its period, T, and in order to be fully specified. also its propagation direction and phase at a given location and time. All these concepts will be introduced below.
Fig. 1: The sine wave
Consider the function ![]() of the two variables position, x, and time, t:
of the two variables position, x, and time, t:
![]()
Convince yourself that this function has the following properties:
• For a fixed ![]() ,
,
![]() is a sine function
of x
is a sine function
of x
• For a fixed ![]() ,
,
![]() is a sine
function of t
is a sine
function of t
•![]() , which
shows that the function repeats itself each time x is increased with
, which
shows that the function repeats itself each time x is increased with
![]() . This explains
why
. This explains
why ![]() is called
wavelength.
is called
wavelength.
•![]() which shows
that the function repeats itself with period T.
which shows
that the function repeats itself with period T.
•![]() provided
provided
![]()
The quantity ![]() is called the wavenumber and is usually denoted by the letter k.
Similarly,
is called the wavenumber and is usually denoted by the letter k.
Similarly, ![]() is
written w (the Greek letter omega )
and called the angular frequency. The unit for k is rad/m and
for w rad/s. Note that f = 1/T
is called frequency and is measured in Hertz (Hz= 1/s).
is
written w (the Greek letter omega )
and called the angular frequency. The unit for k is rad/m and
for w rad/s. Note that f = 1/T
is called frequency and is measured in Hertz (Hz= 1/s).
The constant a in front of the sine is called the amplitude of the wave.
Note that since ![]() ,
,
![]() . That is,
. That is, ![]() is never larger than the amplitude.
is never larger than the amplitude.
The basic feature of the wave as defined above is that the whole pattern
moves along the x-axis as the time changes. Consider for simplicity the
point x = 0, t = 0, where h is
equal to 0. If now t starts to increase, the points ![]() defined by
defined by ![]() will
have the property that
will
have the property that ![]() for all t. The point where h
is 0,
for all t. The point where h
is 0, ![]() , thus
moves with velocity l/T along the x-axis.
The last property stated above shows this in general.
, thus
moves with velocity l/T along the x-axis.
The last property stated above shows this in general.
An additional angle a in the expression ![]() is called a phase term.
is called a phase term.
The argument of the sine, i.e. ![]() ,
is in general called the phase. The phase is often denoted by the letter
f (Greek phi). Since
,
is in general called the phase. The phase is often denoted by the letter
f (Greek phi). Since ![]() phase differences of any multiple of 2p
do not matter at all. The phase of the point
phase differences of any multiple of 2p
do not matter at all. The phase of the point ![]() will be equal to the phase of the point
will be equal to the phase of the point ![]() if
if
![]()
that is,
![]()
or,
![]()
The point ![]() on the x-axis which moves with velocity
on the x-axis which moves with velocity ![]() will therefore experience the same phase for all times. Therefore, the velocity
will therefore experience the same phase for all times. Therefore, the velocity ![]() is called the phase velocity associated with the wave.
is called the phase velocity associated with the wave.
Let us see what happens if we add two general waves, one travelling to the right and one to the left. We first recall the trigonometric identity
![]() )
)
Consider
![]()
This function is a product of a sine and a cosine; the first with x as argument and the second with t. Figure 2 shows a plot of the functions for different t's.
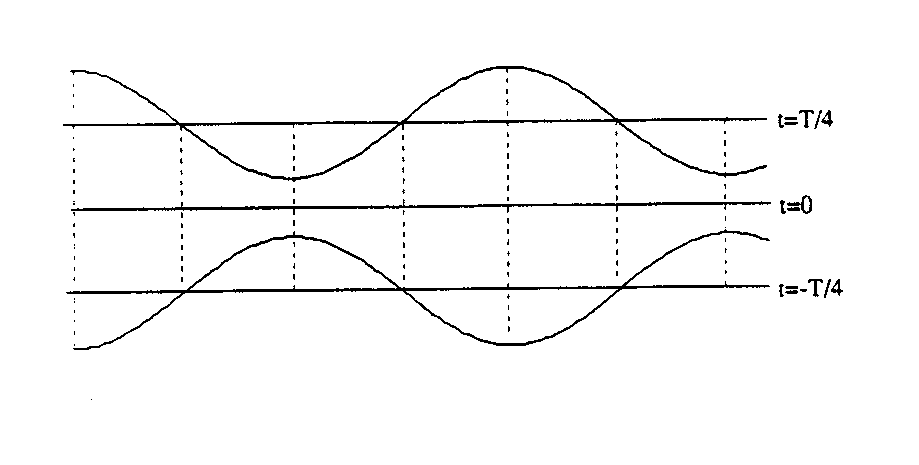
Fig. 2: The standing wave
Note that the function is always 0 for ![]() . In this case we therefore do not have a travelling wave. However, since we still have a periodic behaviour both in x and t, it is customary to call this case a standing wave.
. In this case we therefore do not have a travelling wave. However, since we still have a periodic behaviour both in x and t, it is customary to call this case a standing wave.